Significant figures and grading tolerance

The % grading tolerance setting affects how Mastering grades numeric answers. It determines the range of answers accepted as correct for the acceptable variation or rounding error.

The number of significant figures a student enters in their answer is NOT graded by the system. The significant figures setting determines the properly-formatted answer to which the % tolerance is applied.

The numeric value or symbolic expression and numeric value with units answer types include settings for significant figures and grading tolerance.

Use these format conventions to change numeric correct answers and wrong answers from the default setting of three significant figures. These formats change the value for the correct answer or wrong answer that is used to compare with the student submitted answer.

• For correct answers
  Enter the format in the “Answer format (display of significant figures)” text box in the area for the correct answer(s).
• For wrong answers
  Enter the format in the “Format” text box in the Wrong Answer Feedback area. (Adding wrong answer feedback is optional, but recommended.)

Format	Sample display for 1234.5	Meaning
#	1235	Integer format. Rounds the value to the nearest integer.
#.	1235.	Integer format with trailing decimal point.
#.#	1234.5	Floating point with 2 digits of precision. Additional digits of precision are added by providing more pound signs to the right of the decimal. For example, #.## produces 1234.50.
#.##E+00	1.23*10^03	Scientific notation (same rules for digits of precision as for floating point, described above). The E+00 portion specifies the minimum number of digits for the exponent. To increase the number of exponent digits, add more zeros (for example, E+000).
{2}	1200	Round and display to 2 significant figures, using loose significant figure conventions. (See next section for details.)
[2]	1.2*10^3	Round and display to 2 significant figures, using tight significant figure conventions. (See next section for details.)
[2.]	1.2*10^3	(See next section for details.)

Use these same conventions when you want to set the display of numeric variable values. Changing the display of numeric variable values does not affect the full precision of the variable values used in calculations.

In the following example:

• V is a value expressed as a decimal (e.g., 12345.6789).
• L is the number of digits in V to the left of the decimal place.
• R is the number to the right of the decimal place.
• N is the number of significant digits.

Loose sigfig conventions

Round V to N significant figures. Call this V_r.

If...	Then...
V_r > 10000 or V_r < 0.1	Express V_r in scientific notation with 1 digit left of the decimal and N-1 digits right of the decimal. If N = 1, do not include the decimal point.
1 > V_r >= 0.1	Display as zero+decimal point+N digits right of the decimal point.
N > L	Display all digits to the left of the decimal, a decimal point, and N-L right of the decimal.
N <= L	Display as an integer without any decimal point.

Using loose conventions, 200 is displayed as 200 to 1, 2, or 3 sigfigs.

Tight sigfig conventions WITHOUT trailing-dot notation

Round V to N significant figures. Call this V_r.

If...	Then...
V_r > 10000 or V_r < 0.1	Express V in scientific notation with 1 digit left of the decimal and N-1 digits right of the decimal. If N = 1, do not include the decimal point.
1 > V_r >= 0.1	Display as zero+decimal point+N digits right of the decimal point.
N > L	Display all digits to the left of the decimal, a decimal point, and N-L right of the decimal.
N = L, and the right-most digit before the decimal is not zero	Display as an integer.
N = L, and right-most digit before the decimal is zero	Display using scientific notation.
N < L	Display using scientific notation with 1 digit left of the decimal and N-1 digits right of the decimal
N < L and N = 1	Display using scientific notation. Do not include the decimal point

 

Using tight conventions without trailing-dot notation:

• 1 significant figure – 200
• 2 significant figures – 2.0*10^2
• 3 significant figures – 2.00*10^2
  
  

Tight sigfig conventions WITH trailing dot notation

These are the same as tight without trailing dot except for the last row:

If...	Then...
N = L, and the last digit is zero	Display as an integer and add a decimal point at the end.

 

Using tight conventions with trailing dot notation, 200 is displayed as:

• 1 significant figure – 200
• 2 significant figures – 2.0*10^2
• 3 significant figures – 200. (includes the period)
  
  

Mastering problems set to two or three significant figures are graded most often, though not always, to 2% or 3% tolerance. Answers requiring greater than three-digit precision may be coded with a tighter tolerance. For example, a 0.1% - 0.9% tolerance is typical when four significant figures are required.

In all cases, the answer format is set to redisplay the answer to the proper number of significant figures upon student submission. Whenever appropriate, answer instructions should explicitly state the required number of significant figures.

The ranges of values for which various Mastering responses are given to students are based on the correctly rounded answer and the full precision answer. The full precision answer is the non-rounded answer.

• If the tolerance is set to 2% — The image below shows how Mastering grades student answers for a full-precision answer of 11.4 that is rounded to two significant figures, producing a correctly rounded answer of 11.

  

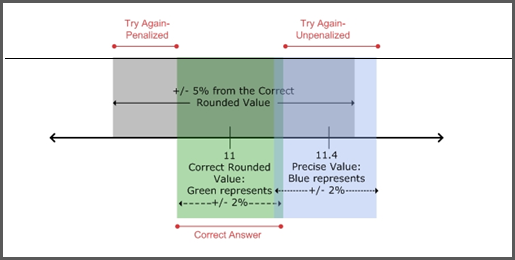
• If the tolerance is set above 2% — The threshold for getting the message Incorrect; Try Again is 5%, straddling the correctly rounded answer.

  

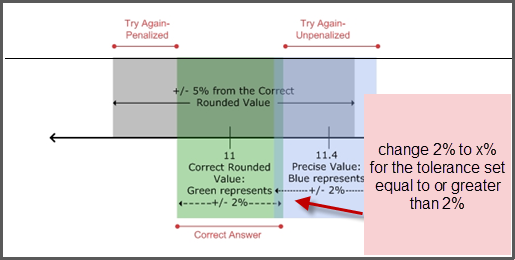
• If the tolerance is set at 5% or above —
  Mastering gives the same feedback Incorrect; Try Again for any value students submit outside this tolerance range. Values within the tolerance percentage (that is, x% straddling the unrounded answer) will give this feedback to students:

  Incorrect; Try Again; no points deducted
  Very close. Check the rounding and number of the significant figures in your final answer.

• If the tolerance is set to below 2% —
  For a tolerance of y%, the threshold for the feedback Incorrect; Try Again is set at beyond 3*y %, straddling the correctly rounded answer. This should take into account that any answer within y% of the unrounded answer will give the following feedback:

  Incorrect; Try Again; no points deducted
  Very close. Check the rounding and number of the significant figures in your final answer.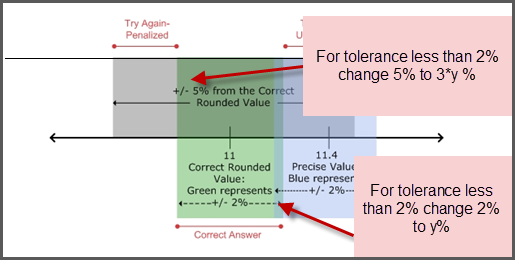

  

To find the upper and lower bounds of different thresholds, you can use the following method (the bounds are exclusive):

• Upper bound = value/(1-0.01*threshold %)
• Lower bound = value*(1-0.01*threshold %)

The "value" in the above expressions could be for the correctly rounded answer with threshold being the tolerance percentage or the 5% threshold (for tolerances greater than or equal to 2%) or the 3*tolerance % threshold (for tolerances less than 2%). The "value" can also be the unrounded answer, where the threshold would be the tolerance percentage.

For more about tolerance range and the answer feedback, see the next section.

The most useful guide is the formula: sigfig = 1+ceiling(-log_10(tolerance))

Set the tolerance based on the guide and the number of significant figures as determined from the values in the problem statement.

Mastering grading compares the student submitted answer to the format set for the correct answer. For a correctly formatted answer "c", a 3% tolerance is calculated as an asymmetric range around "c", as follows:

• The lower end of the range is c*(1-0.03).
• The upper end of the range is c/(1-0.03).

For example, if c=13 and tolerance= 3% or 0.03, then the lower range end of the tolerance range = 13*(1-0.03) = 12.61 exclusive, and the upper end of the tolerance range = 13/(1-0.03) = 13.4021 exclusive. For more details about this example, including grading and answer feedback, see the section "Example of significant figures and tolerance handling" below.

Specifying too few significant figures, combined with too tight a tolerance, can result in student frustration. For example, if an author codes a six-digit answer but has set the format to {3} with a low enough tolerance such that the six-digit answer is now "incorrect". Note the following grading implications and answer feedback scenarios.

 

This example uses an answer formatted to two significant figures with a tolerance of 3% that is coded as theta*r, where theta=8.4 radians and r=1.5 cm. Mastering grades on the full precision answer 12.6 cm and the correctly rounded answer of 13 cm.

This table shows the grading and answer feedback for possible student answers. Note that some of the tolerance ranges overlap. In these cases, the first condition a student answer satisfies is used (i.e., row 2 before row 3, row 3 before row 4).

Student answer	Deviation from full precision answer of 12.6	Deviation from correctly rounded answer of 13	Mastering response
13		0%	Correct
12.62		0 to -3%	Correct Significant Figures Feedback:"Your answer 12.62 was either rounded differently or used a different number of significant figures than required for this part." Show additional rounding message: If the author has specified to show the additional rounding message, this additional also appears: "If you need this result for any later calculation in this item, keep all the digits and round as the final step before submitting your answer."
13.39		0 to +3%	Correct Significant Figures Feedback:"Your answer 13.39 was either rounded differently or used a different number of significant figures than required for this part." Show additional rounding message: If the author has specified to show the additional rounding message, this additional also appears: "If you need this result for any later calculation in this item, keep all the digits and round as the final step before submitting your answer."
12.35		-3 to -5%	Incorrect; Try again; no points deducted Feedback:"Very close. Check the rounding and number of the significant figures in your final answer." Mastering grading action: The student is NOT penalized for this submission. Notes: Because 12.35 is close (within 3%) to the full precision answer of 12.6, the feedback for an answer close to 12.6 takes precedence in this case. If the student's submission happened not to be in the range (within 3%) of the full precision answer of 12.6, then the student would have been penalized and the "Incorrect; Try Again" feedback would have been: "Not quite. Check through your calculations; you may have made a rounding error or used the wrong number of significant figures."
13.65		+3 to +5%	Incorrect; Try again Feedback: "Not quite. Check through your calculations; you may have made a rounding error or used the wrong number of significant figures." Mastering grading action: The student IS penalized for this submission (loss of an answer attempt and any associated credit).
12.6	0%		Incorrect; Try again; no points deducted Feedback:"Very close. Check the rounding and number of the significant figures in your final answer." Mastering grading action: The student is NOT penalized for this submission.
12.23	0 to -3%		Incorrect; Try again; no points deducted Feedback:"Very close. Check the rounding and number of the significant figures in your final answer." Mastering grading action: The student is NOT penalized for this submission.
12.98	0 to +3%		Correct Significant Figures Feedback:"Your answer 12.98 was either rounded differently or used a different number of significant figures than required for this part." Notes: Because 12.98 is close (within 3%) to the correctly rounded answer of 13, the feedback for an answer close to 13 takes precedence in this case. If the student's submission happened not to be in the range (within 3%) of the correctly rounded answer of 13, then the student would have received the "Incorrect; Try Again; no points deducted" feedback: "Very close. Check through your calculations; you may have made a rounding error or used the wrong number of significant figures."
11.97	-3 to -5%		Incorrect; Try again Notes: Because 11.97 is beyond 5% of the correctly rounded answer of 13, Mastering doesn't provide any answer feedback. The student IS penalized for this submission (loss of an answer attempt and any associated credit).
13.23	+3 to +5%		Correct Significant Figures Feedback: "Your answer 13.23 was either rounded differently or used a different number of significant figures than required for this part." Show additional rounding message: If the author has specified to show the additional rounding message, this additional also appears: "If you need this result for any later calculation in this item, keep all the digits and round as the final step before submitting your answer." Notes: Because 13.23 is close (within 3%) to the correctly rounded answer of 13, the feedback for an answer close to 13 takes precedence in this case. If the student's submission happened not to be in the range (within 3%) of the correctly rounded answer of 13, then the student would just see the "Incorrect; Try again" feedback message, similar to the previous answer example of 11.97 above.